$equação Graceli quântica []$

$\psi ^{*}$

equação Graceli tensorial quântica [1]

$T^{\nu }{}_{\alpha }$

$equação Graceli tensorial quântica [2]$

$T^{\nu }{}_{\alpha }$

$\psi ^{*}$

G $T^{\nu }{}_{\alpha }$ [DR] = $F^{\mu \nu }$ $T^{\mu \nu }$ $P^{\mu }\!$ $\eta _{\mu \nu }$ =

EQUAÇÃO QUÂNTICA TENSORIAL GRACELI.

G $T^{\nu }{}_{\alpha }$ [DR] = ${\hat {H}}$ $\left|\psi ({\vec {r}},t)\right\rangle$ $F^{\mu \nu }$ $T^{\mu \nu }$ $P^{\mu }\!$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$

G $T^{\nu }{}_{\alpha }$ [DR] = É O TENSOR GRACELI TENSÃO ENERGIA DE FLUXOS DE DILATAÇÕES E RETRAÇÕES COM CURVATURAS E SIMÉTRICO .

G $T^{\nu }{}_{\alpha }$ [DR] = $F^{\mu \nu }$ $T^{\mu \nu }$ $P^{\mu }\!$ $\eta _{\mu \nu }$ =

G $T^{\nu }{}_{\alpha }$ [DR] = É O TENSOR GRACELI TENSÃO ENERGIA DE FLUXOS DE DILATAÇÕES E RETRAÇÕES COM CURVATURAS E SIMÉTRICO .

G $T^{\nu }{}_{\alpha }$ [DR] = $F^{\mu \nu }$ $T^{\mu \nu }$ $P^{\mu }\!$ $\eta _{\mu \nu }$ / [ $\psi$ $\lambda$ ω $/ T] =$

$T^{\nu }{}_{\alpha }$ ${\sqrt {\frac {2}{\pi }}}$ + $({\frac {\pi }{2}})^{1/2}$ .+ ${\frac {\pi }{2}}t^{2}$ $\psi$

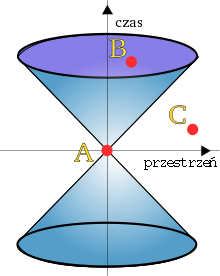
o espaço tempo tensorial Graceli no Espaço de Minkowski .

Em física e matemática, espaço de Minkowski, também tratada de métrica de Minkowski, é a configuração matemática na qual a teoria da relatividade especial de Einstein é mais comumente formulada. Nessa configuração as três dimensões usuais do espaço são combinadas com uma única dimensão do tempo para formar uma variedade quadrimensional para representar um espaço-tempo.

O espaço de Minkowski possui este nome em referência ao matemático alemão Hermann Minkowski.

Estrutura[editar | editar código-fonte]

Formalmente, o espaço de Minkowski é um campo vetorial real quadrimensional equipado com uma forma bilinear simétrica, não degenerada, com assinatura (-,+,+,+).

Elementos do espaço de Minkowski são chamados eventos ou quadrivetores.

Espaço de Minkowski é freqüentemente denotado

$T^{\nu }{}_{\alpha }$ ${\sqrt {\frac {2}{\pi }}}$ + $({\frac {\pi }{2}})^{1/2}$ .+ ${\frac {\pi }{2}}t^{2}$ $\psi$ R^1,3

para enfatizar a assinatura, entretanto é também denotada

$T^{\nu }{}_{\alpha }$ ${\sqrt {\frac {2}{\pi }}}$ + $({\frac {\pi }{2}})^{1/2}$ .+ ${\frac {\pi }{2}}t^{2}$ $\psi$ M⁴

ou simplesmente M.

O Produto interno no espaço de Minkowski[editar | editar código-fonte]

O que se chama de produto interno no espaço de Minkowski é similar ao produto interno euclidiano, com uma diferença fundamental: enquanto que em um produto interno a equação v.v = 0 tem como única solução o vetor nulo v = 0, no caso do espaço de Minkowski existem vários quadrivetores que a satisfazem.

Este produto interno gera uma geometria diferente da euclideana, a geometria geralmente associada a relatividade.

Considere $�$ sendo um vetor-espaço real quadrimensional. O produto interno Minkowski é uma função

$T^{\nu }{}_{\alpha }$ ${\sqrt {\frac {2}{\pi }}}$ + $({\frac {\pi }{2}})^{1/2}$ .+ ${\frac {\pi }{2}}t^{2}$ $\psi$ $\eta :M\times M\rightarrow \mathbb {R}$

(isto é, dado dois vetores quaisquer $�, �$ em $�$ define-se $\eta (V,W)$ como um número real) que satisfaz as propriedades (1), (2), (3) listadas aqui, bem como a propriedade (4) dada abaixo:

$T^{\nu }{}_{\alpha }$ ${\sqrt {\frac {2}{\pi }}}$ + $({\frac {\pi }{2}})^{1/2}$ .+ ${\frac {\pi }{2}}t^{2}$ $\psi$ bilinear: $\eta (aU+V,W)\,=a\eta (U,W)+\eta (V,W)$ , ( $\forall a\in \mathbb {R}$ e $\forall U,V,W\in M$ )

2. simétrica:

$\eta (V,W)\,=\eta (W,V)$ ( $\forall V,W\in M$ )

3. não degenerada: se

$T^{\nu }{}_{\alpha }$ ${\sqrt {\frac {2}{\pi }}}$ + $({\frac {\pi }{2}})^{1/2}$ .+ ${\frac {\pi }{2}}t^{2}$ $\psi$

$\eta (V, W) \, = 0$ $\forall W \in M$ , então $V \, = 0$ ,

4. O produto interno $\eta$ tem assinatura métrica (-,+,+,+)

Uma forma bilinear simétrica em um espaço vetorial V sobre um corpo K é uma função $B:V\times V\to K\,$ satisfazendo:^[1]

B é uma forma bilinear, ou seja
- $B(u+u',v)=B(u,v)+B(u',v)\,$
- $B(u,v+v')=B(u,v)+B(u,v')\,$
- $B(\lambda u,v)=B(u,\lambda v)=\lambda \,B(u,v)\,$
B é simétrica, ou seja
- $B(u,v)=B(v,u)\,$

Formas bilineares simétricas são importantes no estudo das quádricas e na teoria da relatividade, em que o "produto interno" é uma forma bilinear simétrica não-degenerada.

Em matemática, um espaço de Banach, é um espaço vectorial normado completo. Deve seu nome ao matemático polaco Stefan Banach(1892-1945), o qual contribuiu para a teoria das séries ortogonais e inovações na teoria de medida e integração, sendo a sua contribuição mais importante na análise funcional.

Definições preliminares[editar | editar código-fonte]

Espaços métricos[editar | editar código-fonte]

Sejam $�$ um conjunto não-vazio e $�$ uma métrica em $�$ , dizemos que o par ( $�$ , $�$ ) é um espaço métrico.

Espaço vetorial normado[editar | editar código-fonte]

Seja $�$ um espaço vectorial sobre um corpo e $\|.\|$ uma norma de $�$ . O par ( $�$ , $\|.\|$ ) é um espaço vetorial normado.

Um espaço normado ( $�$ , $\|.\|$ ) pode ser considerado um espaço métrico ( $�$ , $�$ ), basta definir a seguinte métrica

d(x,y)=\|x-y\|

, para todo

\ x,\ y\in E

De fato, os axiomas da métrica são satisfeitos. Assim, para todo $\ x,\ y,\ z\in E$ , resulta:

• $d(x,x)=\|x-x\|=\|0\|=0$ ; •Se $x\neq y$ e $x>y$ , então $\|x-y\|=x-y>0$ , $d(x,y)>0$ .

Para o caso de $x<y$ , temos: $\|x-y\|=-(x-y)=y-x>0$ ;

• $d(x,y)=\|x-y\|=\|(-1)(y-x)\|=|-1|.\|y-x\|=|1|.\|y-x\|=\|y-x\|=d(y,x)$ ;

• $d(x,z)=\|x-z\|=\|x+(-y+y)-z\|=\|(x-y)+(y-z)\|\leq \|x-y\|+\|y-z\|$ .

Assim, todo espaço normado ( $�$ , $\|.\|$ ) é um espaço métrico ( $�$ , $�$ ), com $�$ sendo a métrica induzida pela norma $\|.\|$ . De modo particular, todo espaço normado é um espaço topológico.

É possível mostrar também que se $�$ $E$ é um espaço vetorial sobre os reais, munido de uma métrica $�$ $d$ , essa métrica é induzida por uma norma se, e somente se, satisfaz:
2. ${\textstyle d(\lambda x,\lambda y)=\vert \lambda \vert d(x,y),\;\forall \lambda \in \mathbb {R} ;\;\forall x,y\in E;}$
4. $d(x+z,y+z)=d(x,y),\;\forall x,y,z\in E.$ $T^{\nu }{}_{\alpha }$ ${\sqrt {\frac {2}{\pi }}}$ + $({\frac {\pi }{2}})^{1/2}$ .+ ${\frac {\pi }{2}}t^{2}$ $\psi$ $d(x+z,y+z)=d(x,y),\;\forall x,y,z\in E.$

Sequência de Cauchy[editar | editar código-fonte]

Uma sequência $(x_{n})$ em um espaço métrico $�$ chama-se uma sequência de Cauchy quando, para todo $\epsilon >0$ dado, existe $n_{0}\in \mathbb {N}$ tal que $m,n>n_{0}$ implica $d(x_{m},x_{n})<\epsilon$ .

Intuitivamente, à medida que o índice $�$ cresce, os termos da sequência de Cauchy se tornam mais próximos.

Toda sequência convergente é de Cauchy.
Toda sequência de Cauchy é limitada.

Espaços métricos completos[editar | editar código-fonte]

Um espaço métrico $�$ é completo quando toda sequência de Cauchy em $�$ é convergente em $�$ .

Para mostrar que um espaço métrico $�$ não é completo, basta mostrar que existe uma sequência de Cauchy em $�$ que não seja convergente.
O espaço métrico $\mathbb {Q}$ não é completo. Basta tomar uma sequência de números racionais $(x_{n})$ convergindo para um número irracional $�$ . Por exemplo, $x_{1}=1;x_{2}=1,4;x_{3}=1,41;x_{4}=1,414...,$ com $\lim x_{n}={\sqrt {2}}$ . Assim, $(x_{n})$ é uma sequência de Cauchy no espaço métrico $\mathbb {Q}$ , mas não é convergente em $\mathbb {Q}$ .

Definição[editar | editar código-fonte]

Um espaço vectorial normado $�$ é chamado Espaço de Banach quando for um espaço métrico completo, ou seja, se toda sequência de Cauchy em $�$ é convergente em $�$ .

Quando queremos mostrar que um espaço é normado, a principal dificuldade ocorre em se demonstrar a desigualdade triangular. Há algumas desigualdades que nos auxiliam bastante neste processo:

Desigualdade de Young[editar | editar código-fonte]

Dados $a,b\in \mathbb {R} ,\;p,q\in (1,+\infty )$ tais que $a,b>0{\text{ e }}{\frac {1}{p}}+{\frac {1}{q}}=1$ (dizemos que $p{\text{ e }}q$ são conjugados de Hölder)¨, vale a desigualdade:

$ab\leqslant {\frac {a^{p}}{p}}+{\frac {b^{q}}{q}}.$

Desigualdade de Hölder[editar | editar código-fonte]

Dados $x=(x_{1},x_{2},\cdots ,x_{n}),\;y=(y_{1},y_{2},\cdots ,y_{n})\in \mathbb {R} ^{n},\;p,q\in (1,+\infty )$ conjugados de Hölder, vale a desigualdade:

$T^{\nu }{}_{\alpha }$ ${\sqrt {\frac {2}{\pi }}}$ + $({\frac {\pi }{2}})^{1/2}$ .+ ${\frac {\pi }{2}}t^{2}$ $\psi$

$\sum _{i=1}^{n}\vert x_{i}y_{i}\vert \leqslant \left(\sum _{i=1}^{n}\vert x_{i}\vert ^{p}\right)^{\frac {1}{p}}\left(\sum _{i=1}^{n}\vert y_{i}\vert ^{q}\right)^{\frac {1}{q}}.$

Se definimos um produto coordenada a coordenada em $\mathbb {R} ^{n}$ da forma $xy=(x_{1}y_{1},x_{2}y_{2},\cdots ,x_{n}y_{n})$ , podemos reescrever a desigualdade como:

$\Vert xy\Vert _{1}\leqslant \Vert x\Vert _{p}\Vert y\Vert _{q}.$

Desigualdade de Minkowski[editar | editar código-fonte]

Dados $x,y\in \mathbb {R} ^{n}{\text{ e }}p\in (1,+\infty )$ , vale a desigualdade:

$\Vert x+y\Vert _{p}\leqslant \Vert x\Vert _{p}+\Vert y\Vert _{p}.$

Propriedades[editar | editar código-fonte]

Se $�$ é espaço vetorial normado, e $Y\subseteq X$ é subespaço vetorial, então $�$ é um espaço vetorial normado, com norma herdada do espaço $�$ .
Se $�$ é espaço de Banach e $Y\subseteq X$ é subespaço vetorial, então $�$ é espaço de Banach se, e somente se, $�$ é fechado em $�$ .
Para todo espaço vetorial normado $�$ , é possível estender a norma de forma que o completamento de $�$ , denotado ${\widetilde {X}}$ , seja espaço vetorial normado completo, ou seja, ${\widetilde {X}}$ é espaço de Banach.

Pesquisar este blog

TENSOR , GEOMETRIA, TOPOLOGIA, espaço tensorial, VARIEDADE DE GRACELI [2]

o espaço tempo tensorial Graceli no Espaço de Minkowski .

Estrutura[editar | editar código-fonte]

O Produto interno no espaço de Minkowski[editar | editar código-fonte]

Definições preliminares[editar | editar código-fonte]

Espaços métricos[editar | editar código-fonte]

Espaço vetorial normado[editar | editar código-fonte]

Sequência de Cauchy[editar | editar código-fonte]

Espaços métricos completos[editar | editar código-fonte]

Definição[editar | editar código-fonte]

Desigualdade de Young[editar | editar código-fonte]

Desigualdade de Hölder[editar | editar código-fonte]

Desigualdade de Minkowski[editar | editar código-fonte]

Propriedades[editar | editar código-fonte]

Comentários

Postar um comentário

Postagens mais visitadas deste blog